News
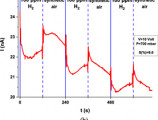
The peer-reviewed research paper entitled “Self-powered, flexible and room temperature operated solution processed hybrid metal halide p-type sensing element for efficient hydrogen detection”, resulting from a collaboration between the Institute of Electronic Structure and Laser (IESL–FORTH), the University of Crete, and the Hellenic Mediterranean University (HMU), has been selected for inclusion in a curated collection of JPhys Materials (IOP Publishing).
The Soft Matter Division of IESL-FORTH demonstrated its scientific excellence during the 15th Hellenic Polymer Society International Conference (POLYCONF15), held in Patras during December 3-6, 2025.
We are thrilled to announce the pioneering publication of the Photonics for Heritage Science group at IESL - FORTH: “Machine learning assisted real-time acoustic monitoring of laser cleaning in Heritage conservation” by Georgios D. Barmparis, A.-N. Raikidis, Kristalia Melessanaki, G. P. Tsironis, George Tserevelakis, and Paraskevi Pouli. This work paves the way for smart, informed, data-driven restoration technologies, merging AI innovation with the preservation of cultural heritage — where science and heritage converge.